Architecture and Inner Workings

Core Components of a ZK Coprocessor

A ZK Coprocessor consists of several fundamental components that work together to offload computation while preserving verifiability. At the heart of the system is the execution environment, often implemented as a zero‑knowledge virtual machine (zkVM) or a domain‑specific circuit compiler. This environment interprets code or computational tasks and converts them into an arithmetic circuit suitable for zero‑knowledge proof generation.

The prover is the entity that performs the computation and generates the cryptographic proof. It takes the input data, executes the required logic off‑chain, and constructs a succinct proof that attests to the correctness of the computation without revealing sensitive details. The verifier, typically a smart contract deployed on the target blockchain, checks this proof using minimal resources. By design, verification is far less computationally demanding than the original calculation, enabling efficient on‑chain validation.

A supporting component is the data interface, which handles how the coprocessor accesses information from different sources. Some coprocessors query on‑chain data directly, while others aggregate historical or external datasets, such as decentralized storage networks or off‑chain APIs. The integrity of this data must also be provable, often through Merkle proofs or similar cryptographic commitments.

Flow of Computation

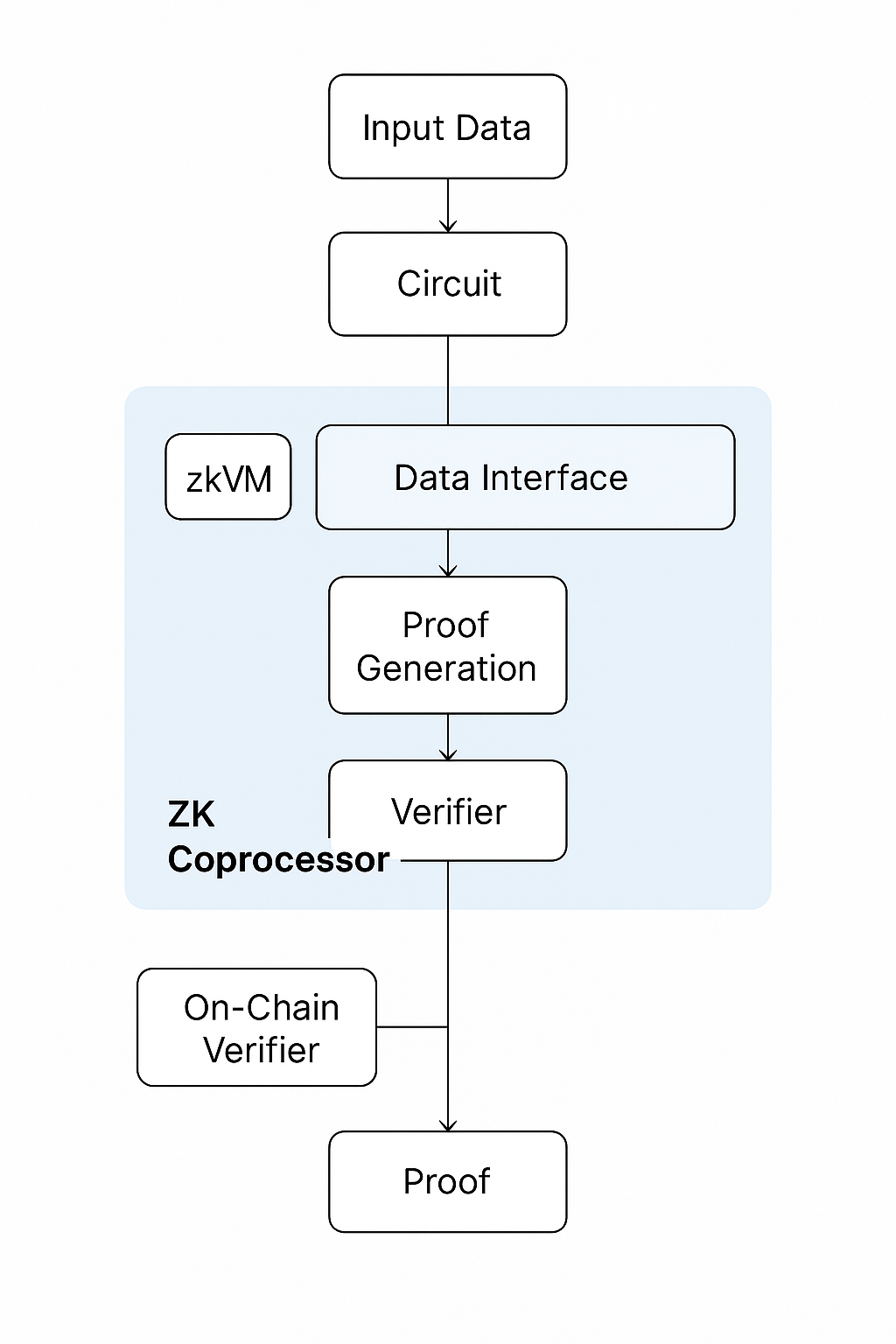
The operation of a ZK Coprocessor follows a clear sequence that separates heavy computation from lightweight verification. The process begins when a decentralized application or smart contract requests a computation that cannot be efficiently performed on‑chain. This request is sent to the coprocessor, which collects the necessary inputs, either from the blockchain’s state, external data feeds, or user‑provided sources.

Once the inputs are assembled, the coprocessor executes the computation within its zkVM or circuit environment. During this step, the computation is transformed into a structured arithmetic circuit, enabling the generation of a zero‑knowledge proof. This proof summarizes the entire execution process in a way that can be checked without re‑running the computation itself.

After the proof is generated, it is transmitted back to the blockchain. The verifier smart contract then validates the proof using publicly known verification keys. If the proof is valid, the result of the computation is accepted and can be used to update on‑chain state, trigger smart contract logic, or serve as an input for further decentralized processes. This flow ensures that computational integrity is maintained without sacrificing efficiency.

Proof Generation Techniques

Proof generation is the most computationally intensive aspect of the ZK Coprocessor architecture. It relies on advanced cryptographic methods such as polynomial commitments and multi‑scalar multiplications, which transform a computation into a set of algebraic constraints. These constraints are then solved to produce a succinct proof.

Modern systems optimize this process through several techniques. Fast Fourier Transforms (FFT) or Number Theoretic Transforms (NTT) are used to accelerate polynomial operations, which are central to zk‑SNARK and zk‑STARK constructions. Recursion is another technique gaining prominence, allowing proofs to be nested within other proofs. Recursive proof systems enable incremental verification, where large computations are broken down into smaller proofs that are subsequently aggregated into a single succinct verification.

These optimizations are crucial for scaling ZK Coprocessors to real‑world workloads. Without them, proof generation could become prohibitively slow or resource‑intensive, undermining the advantages of off‑chain computation.

On‑Chain Verification

The verification phase occurs on the target blockchain and is intentionally designed to be minimal in computational cost. Once the coprocessor submits a proof, the verifier contract runs a verification algorithm using pre‑computed parameters. In zk‑SNARK systems, this often involves a constant‑time pairing check, while zk‑STARK verifiers rely on hash‑based commitments and FRI (Fast Reed‑Solomon Interactive Oracle Proofs of Proximity) protocols.

The succinctness of zero‑knowledge proofs means that verification typically requires only a few kilobytes of data and can be executed within a fraction of the gas required for equivalent on‑chain computation. This efficiency is what makes ZK Coprocessors viable in production environments. The proof confirms not only the correctness of the computation but also the integrity of the inputs and the determinism of the output.

Security Model and Threats

The security of ZK Coprocessors rests on both cryptographic soundness and system design. Cryptographically, their guarantees depend on the hardness of underlying problems, such as elliptic curve pairings or hash‑based commitments. As long as these primitives remain secure, the proofs they generate cannot be forged.

However, vulnerabilities can arise in how the coprocessor is implemented or how data is sourced. A malicious prover could attempt to bypass constraints in the circuit or feed incorrect data into the computation. To mitigate this, coprocessors often rely on public input commitments, Merkle roots, or trusted data feeds to prove that the inputs used were legitimate. Auditing of circuits and rigorous formal verification are also essential to prevent errors in the design itself.

The broader system must also address liveness and availability. If the coprocessor is centralized or controlled by a single operator, it introduces potential trust assumptions or censorship risks. Emerging designs aim to decentralize coprocessor networks, enabling multiple provers to compete or collaborate in generating proofs, thereby reducing reliance on any single entity.